数据结构与算法

Posted 2025-01-14 Updated 2025-01- 13

By Administrator

26~33 min read

算法定义

算法（algorithm）是在有限时间内解决特定问题的一组指令或操作步骤，它具有以下特性。

问题是明确的，包含清晰的输入和输出定义。
具有可行性，能够在有限步骤、时间和内存空间下完成。
各步骤都有确定的含义，在相同的输入和运行条件下，输出始终相同。

数据结构定义

数据结构（data structure）是组织和存储数据的方式，涵盖数据内容、数据之间关系和数据操作方法，它具有以下设计目标。

空间占用尽量少，以节省计算机内存。
数据操作尽可能快速，涵盖数据访问、添加、删除、更新等。（增删改查）
提供简洁的数据表示和逻辑信息，以便算法高效运行。

数据结构设计是一个充满权衡的过程。如果想在某方面取得提升，往往需要在另一方面作出妥协。下面举两个例子。

链表相较于数组，在数据添加和删除操作上更加便捷，但牺牲了数据访问速度。
图相较于链表，提供了更丰富的逻辑信息，但需要占用更大的内存空间。

数据结构无处不在：

地铁路线：图
社会组织形式：树（二叉树、二叉平衡树、红黑树）
冬天的衣服：栈（先进后出）
羽毛球：队列（先进先出）
字典：就是哈希表

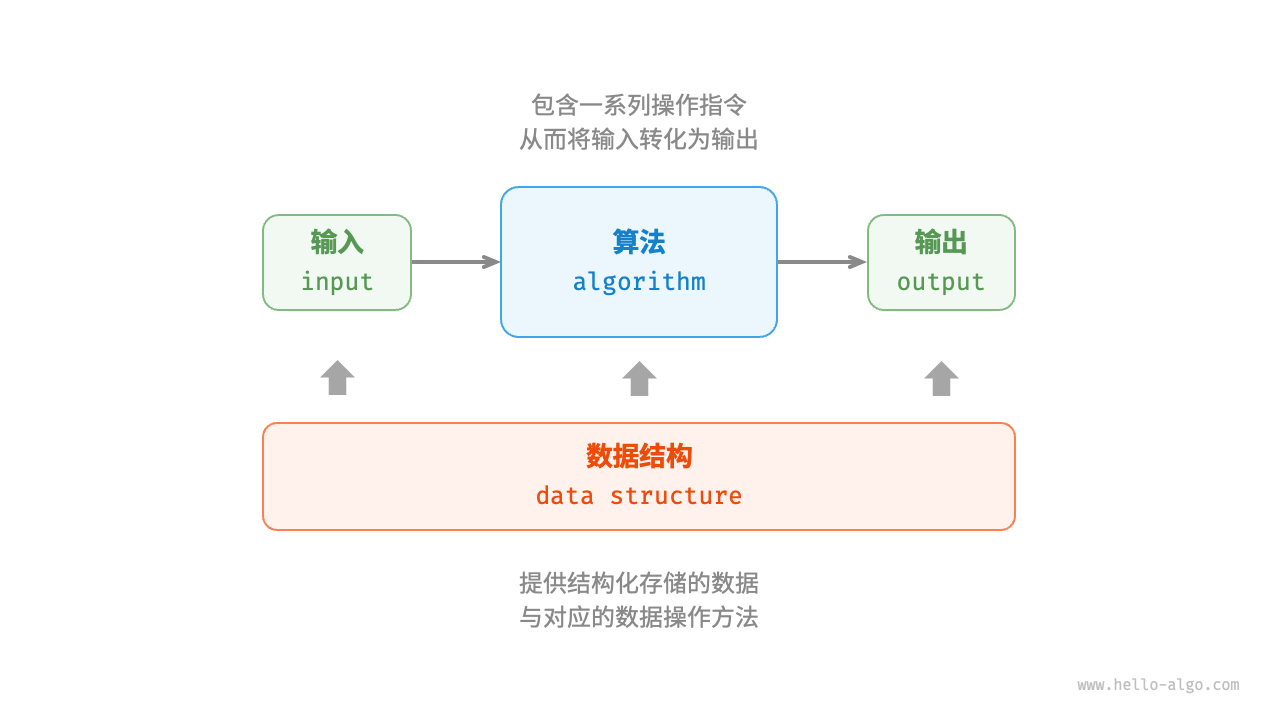
数据结构与算法的关系

如图 1-4 所示，数据结构与算法高度相关、紧密结合，具体表现在以下三个方面。

数据结构是算法的基石。数据结构为算法提供了结构化存储的数据，以及操作数据的方法。
算法为数据结构注入生命力。数据结构本身仅存储数据信息，结合算法才能解决特定问题。
算法通常可以基于不同的数据结构实现，但执行效率可能相差很大，选择合适的数据结构是关键。

图 1-4 数据结构与算法的关系

数据结构与算法犹如图 1-5 所示的拼装积木。一套积木，除了包含许多零件之外，还附有详细的组装说明书。我们按照说明书一步步操作，就能组装出精美的积木模型。

图 1-5 拼装积木

两者的详细对应关系如表 1-1 所示。

表 1-1 将数据结构与算法类比为拼装积木

数据结构与算法	拼装积木
输入数据	未拼装的积木
数据结构	积木组织形式，包括形状、大小、连接方式等
算法	把积木拼成目标形态的一系列操作步骤
输出数据	积木模型

值得说明的是，数据结构与算法是独立于编程语言的。正因如此，本书得以提供基于多种编程语言的实现。

约定俗成的简称

在实际讨论时，我们通常会将“数据结构与算法”简称为“算法”。比如众所周知的 LeetCode 算法题目，实际上同时考查数据结构和算法两方面的知识。

网站：https://www.hello-algo.com/chapter_introduction/what_is_dsa/#123

时间复杂度

重点大O表示法：渐近上界。（获取函数的增加趋势。）

1. 第一步：统计操作数量

针对代码，逐行从上到下计算即可。然而，由于上述 c⋅f(n) 中的常数项 c 可以取任意大小，因此操作数量 T(n) 中的各种系数、常数项都可以忽略。根据此原则，可以总结出以下计数简化技巧。

忽略 T(n) 中的常数项。因为它们都与 n 无关，所以对时间复杂度不产生影响。
省略所有系数。例如，循环 2n 次、5n+1 次等，都可以简化记为 n 次，因为 n 前面的系数对时间复杂度没有影响。
循环嵌套时使用乘法。总操作数量等于外层循环和内层循环操作数量之积，每一层循环依然可以分别套用第 1. 点和第 2. 点的技巧。

2. 第二步：判断渐近上界

时间复杂度由 T(n) 中最高阶的项来决定。这是因为在 n 趋于无穷大时，最高阶的项将发挥主导作用，其他项的影响都可以忽略。

总结：

忽略常数和常数项
只保留最高阶
每一个循环都是用以上规则，最后再将保留下的相加，再保留最高阶。

常见类型

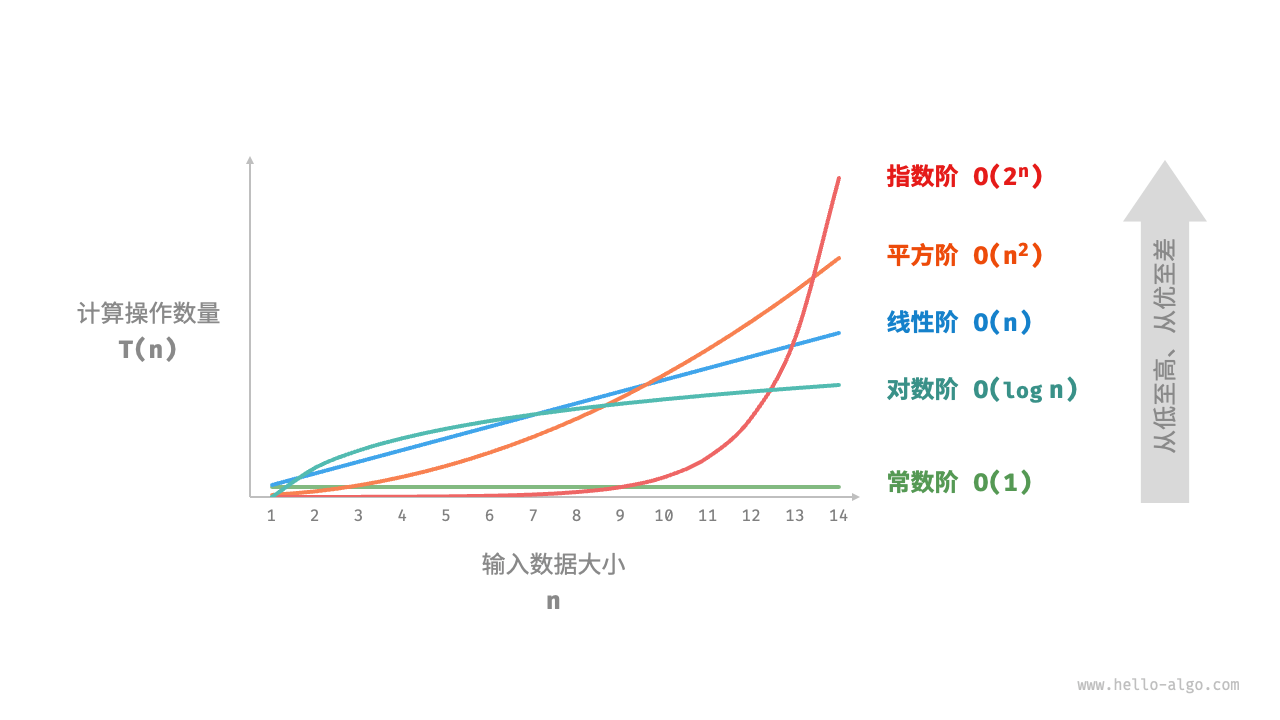
设输入数据大小为 n ，常见的时间复杂度类型如图 2-9 所示（按照从低到高的顺序排列）。

常数阶对数阶线性阶线性对数阶平方阶指数阶阶乘阶常数阶对数阶线性阶线性对数阶平方阶指数阶阶乘阶O(1)<O(log⁡n)<O(n)<O(nlog⁡n)<O(n2)<O(2n)<O(n!)常数阶<对数阶<线性阶<线性对数阶<平方阶<指数阶<阶乘阶

记忆：常对线平指阶

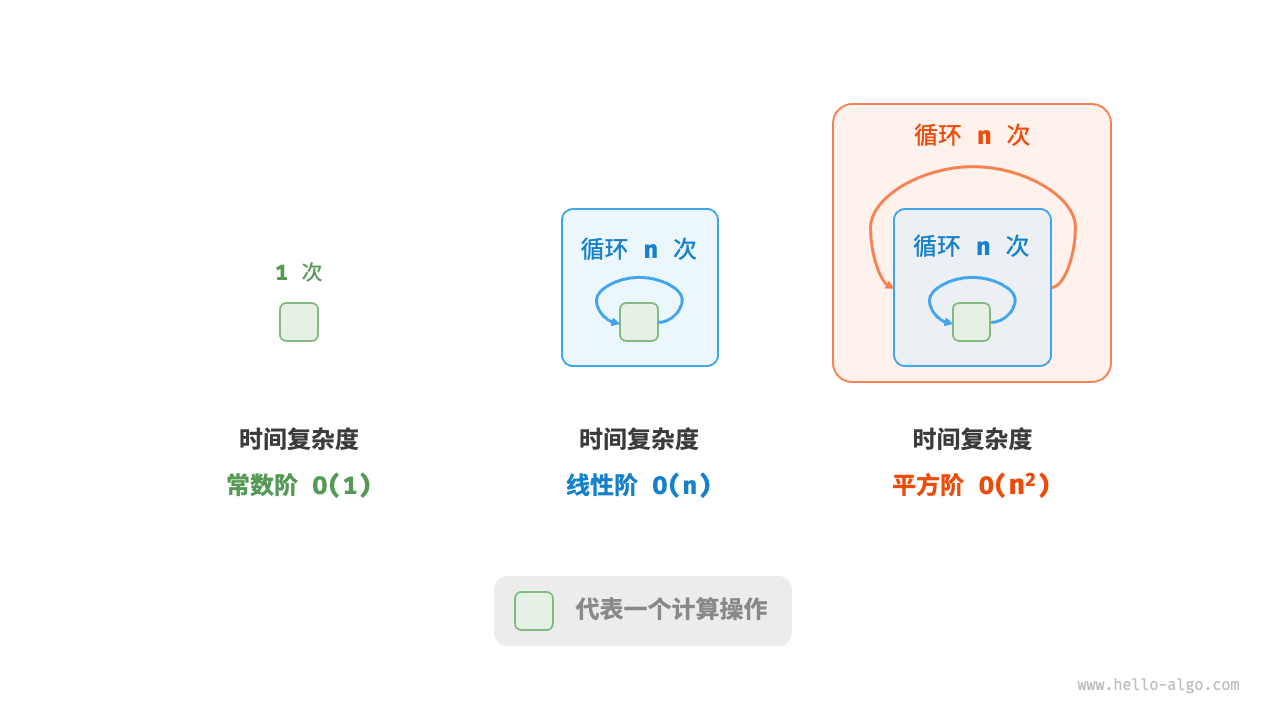
平方阶 O(n2)

平方阶的操作数量相对于输入数据大小 n 以平方级别增长。平方阶通常出现在嵌套循环中，外层循环和内层循环的时间复杂度都为 O(n) ，因此总体的时间复杂度为 O(n2) ： ( 循环嵌套 )

/* 平方阶 */
int quadratic(int n) {
    int count = 0;
    // 循环次数与数据大小 n 成平方关系
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            count++;
        }
    }
    return count;
}

图 2-10 对比了常数阶、线性阶和平方阶三种时间复杂度。

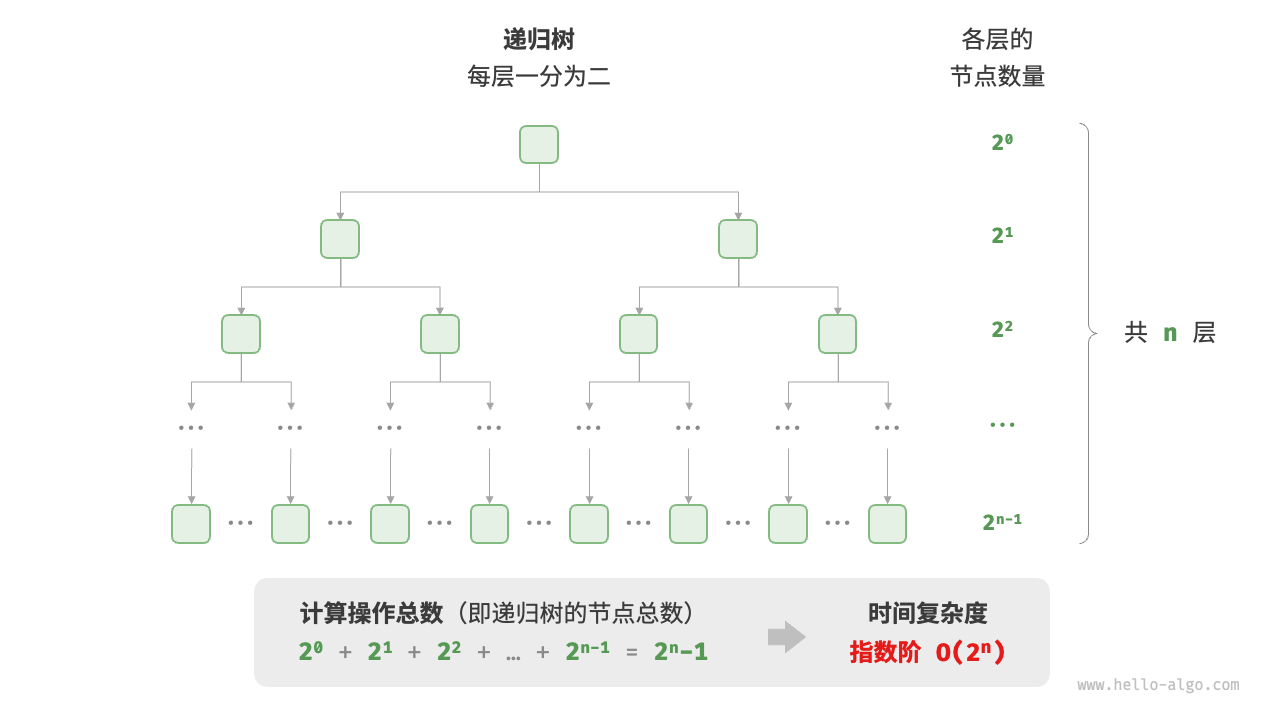
指数阶 O(2n)

生物学的“细胞分裂”是指数阶增长的典型例子：初始状态为 1 个细胞，分裂一轮后变为 2 个，分裂两轮后变为 4 个，以此类推，分裂 n 轮后有 2n 个细胞。

图 2-11 和以下代码模拟了细胞分裂的过程，时间复杂度为 O(2n) 。请注意，输入 n 表示分裂轮数，返回值 count 表示总分裂次数。

对数阶 O(log⁡n)

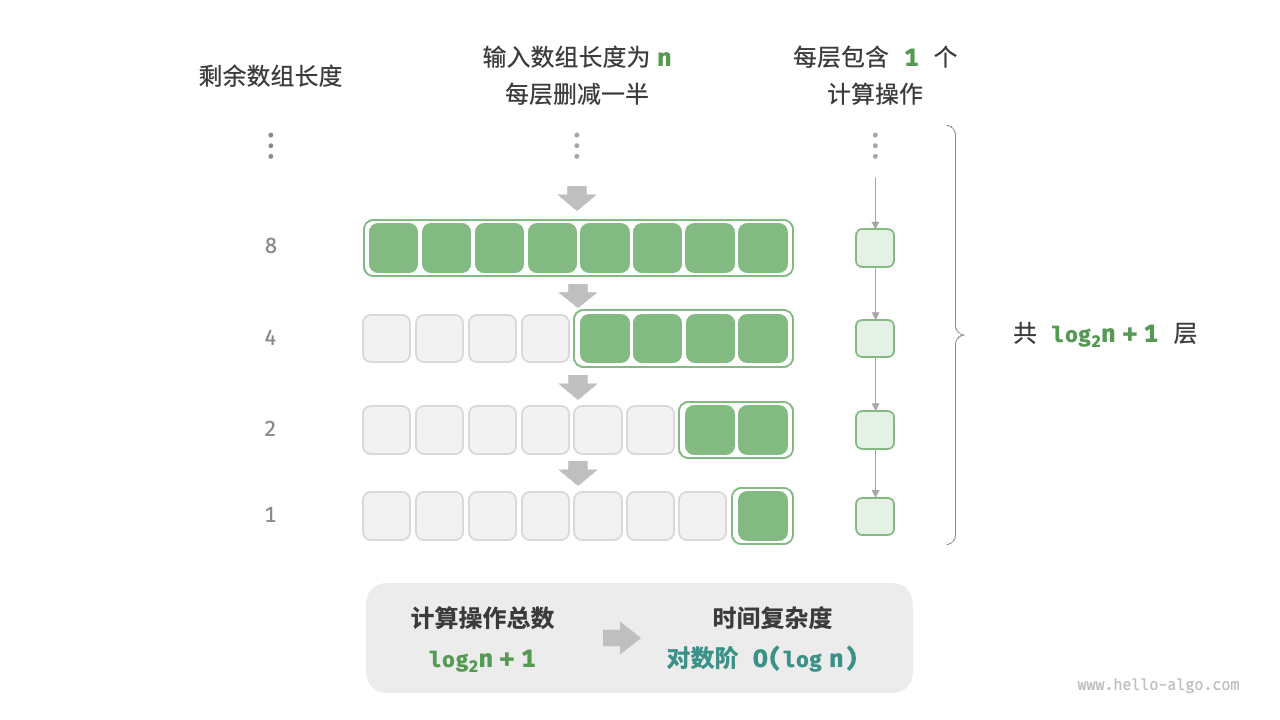
与指数阶相反，对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为 n ，由于每轮缩减到一半，因此循环次数是 log2⁡n ，即 2n 的反函数。

指数转对数：2 ^ x = n ==> log2(n) = x ==> log(n)

图 2-12 和以下代码模拟了“每轮缩减到一半”的过程，时间复杂度为 O(log2⁡n) ，简记为 O(log⁡n) ：

/* 对数阶（循环实现） */
int logarithmic(int n) {
    int count = 0;
    while (n > 1) {
        n = n / 2;
        count++;
    }
    return count;
}

图 2-12 对数阶的时间复杂度

线性对数阶 O(nlog⁡n)

线性对数阶常出现于嵌套循环中，两层循环的时间复杂度分别为 O(log⁡n) 和 O(n)

time_complexity.c

/*
线性对数阶  ，
    执行n 次后返回count 指

    n = 1
    count = 1

    n = 2

    count 1 + 1 + 2 = 4

    n = 3

    count = 1 + 1 + 3 = 5

    n = 4

    count= 1+ 1 + 1 + 1 +  2 + 2 + 4


    n = 6 
   count = 1 + 1 + 1 + 1 + 3 + 3 + 6 
 */
int linearLogRecur(int n) {
    if (n <= 1)
        return 1;
    int count = linearLogRecur(n / 2) + linearLogRecur(n / 2);
    for (int i = 0; i < n; i++) {
        count++;
    }
    return count;
}

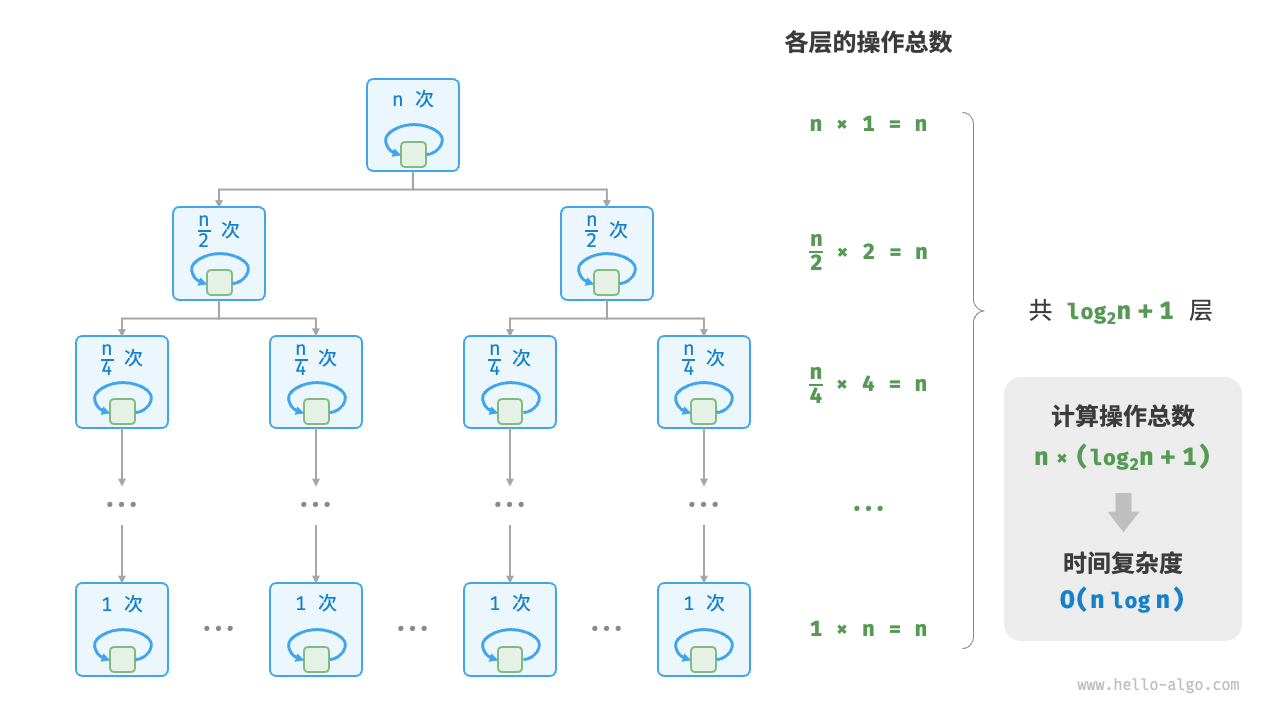
图 2-13 展示了线性对数阶的生成方式。二叉树的每一层的操作总数都为 n ，树共有 log2⁡n+1 层，因此时间复杂度为 O(nlog⁡n) 。

图 2-13 线性对数阶的时间复杂度

主流排序算法的时间复杂度通常为 O(nlog⁡n) ，例如快速排序、归并排序、堆排序等。

一般考虑：最差情况。

空间复杂度

数据结构与算法

License: CC BY 4.0